この課外時間では、数学を使っただけで簡単に「記憶」のモデルができるという話をしよう。 この講義で習った知識を使っただけで簡単な脳のモデルができるんだ。神経細胞がたった3個からなる模型。ほんとの脳ははるかに複雑だけど、ここでは単純化したネットワークを考えてみよう。 まず、モデルの話をする前に、ちょっと基礎練習をしてみよう。いま、この図のように、2つの神経が結合している。 こんな感じで神経1は神経2とシナプスを作っている。丸が神経で、矢印がシナプスの記号。この場合は神経1が送信側で、神経2が受信側だ。つまり信号は神経1から2へ行く。 この図で重要なのは何かというと、2つの神経が結びつく強さだ。この強さを「a」と書こうか。つまり、a という記号はシナプスの強さを表す変数だ。この数値が大きければ大きいほど、シナプスで強く結ばれていることになる。つまり信号が通りやすい。 変数 a は状況に応じて変化するんだけど、その変化の仕方には法則がある。それを「ヘブの法則」っていうんだったね。簡単にいえば「神経1と神経2が同時に活動したときに結合が強くなる」という話だ。つまり、a の値がいま「0」だったとしたら、もし2つの神経が同時に活動したら 0+1 で「1」に増えるわけだ。さらにもう1回、同時に活動したら 1+1 で「2」になる。 でも、ヘブの法則にはその裏のパターンもあって、神経が同時に活動しなかったら、こんどは逆に a を減らすんだ。一種の罰みないなものかな。つまり、a はいまの「2」から「1」に減ってしまう。 さて、神経は2つの状態しか取り得ないね。つまり活動してるか活動してないかの2つ。これも数値化しちゃおう。たとえば、活動してるときを「1」、活動してないときを「-1」で表してみよう。 ── 生徒 え?「-1」……? ゼロでもいいよ。でも、今回はゼロは活動すべきかどうか迷っているという風にかんがえて、あえて「-1」としてみよう。 すると、例えば、両方とも神経が活動した時は「1」を縦に 2つ並べて、 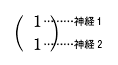 のようにベクトルで表すことができるよね。わかるかな。つまり、このベクトルが起こったら、a が 1 だけ増えるってわけだ。 同じようにして考えると、逆に 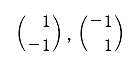 の2つの場合には、a は減るし、 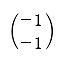 の時には a は変化しないわけだね。 さてと。ここまでが準備だ。これから本題に入ろうか。 今日、試してみる脳のモデルは3個の神経からできている。これを図で表すとこうなる。 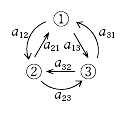 ちょっと複雑に見えるけど、別に難しいことはなくて、ここには神経1, 2, 3と全3つあって、それぞれが相互に手を持っているから、全部で6個のシナプスができるよね。それで、それぞれのシナプスの強さを a12 とか a23 とかって表しているわけ。a12 は神経1から神経2に向かうシナプスの強さという意味ね。 これぐらいだったらまだ数学アレルギーは起こらないよな。というわけで、この図はちょっと見にくいので、簡単にする目的で、こうやって「行列」を使って書こう。 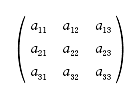 ── 生徒 あれ? a11 とは……。 さっきの図にはなかったね。だから、a11、a22、a33 の対角線の3つはいつでもゼロだと思ってもらえばいい。 さて、初めの脳の状態は全部ゼロだとしようか。つまりこうだ。 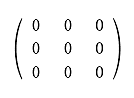 初期状態、何も知らない赤ちゃんの脳だと思ってね。 一方、神経の活動はベクトルで表された。たとえば、 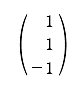 と書いたら、神経1と神経2は活動していて、神経3は活動していないってわけだ。そうだなあ、この(1, 1, -1)の活動の組み合わせをパターンAと呼ぼうか。 さて、3つの神経からなるネットワークに、パターンAの活動が起こりました。そしたら、さっきの「ヘブの法則」を使うと、この行列の中の数値が変化するよね。わかるかな。 もう1回説明しようか。たとえば、パターンAでは神経1と2が同時に活動してるから、a12 とa21 が強まるよね。一方で、神経2と3は一方しか活動してないから、a23 と a32 は弱まるよね。そんな感じで、パターンAが現れると、結果として、行列は  と変化するんだ。だから、たとえばパターンAが3回連続で現れたら、 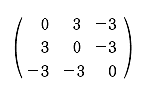 となるよね。 行列がパターンAに曝露されて変化した。つまり可塑性ってやつだ。 さて、つぎなる問題が、じゃあこの行列に何ができるのかってことだ。わかるかな? そう。この行列はパターンAを思い出すことができるんだ。 思い出すというのは行列の「かけ算」でする。たとえばパターンA(1, 1, -1)を思い出したかったら、 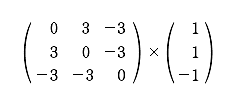 と、やればいい。どう? 数学の授業で習った行列の計算は覚えてるかな? 答えはこうなるね。 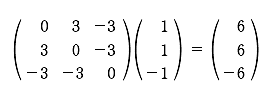 できたかな? ここで「6」とか「−6」とかという数字がでてきたね。でも、神経ってやつは「1」と「-1」しか取りえないから、正の数だったら「1」と同じだと思って、逆に、負の数だったら「-1」と同じだと考えるんだな。そうするとどう? 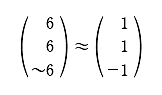 ほら、思い出してるでしょ。最初に覚えたパターンA(1, 1, -1)と同じじゃん。わかった? すごいよね。行列が覚えたことを思い出すことができるんだからさ。 でも、これで驚いちゃいけない。この脳モデルはまだいろいろなことができるんだ。 じゃあ、次に新しいパターンを教えてみようか。たとえば、パターンBとして 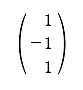 この新しいパターンのベクトルを使ってみよう。すでにパターンAを3回学習した行列に、このパターンBを2回連続で教えると、 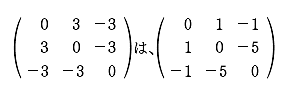 となるよね。もう慣れて楽に計算できるようになったかな。 さてここで、この新しい行列が最初のパターンA(1, 1, -1)をいまでも覚えているかを確認してみよう。 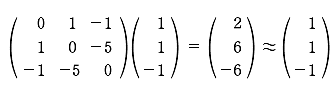 ── 生徒 ああ……。 ほら、(1, 1, -1)だ。まだ、ちゃんとパターンAを思い出せるね。行列の中身がすっかり変わってしまったのに、まだ記憶しているなんてほんとうに見事だ。 じゃあ、2つ目に覚えたやつ、パターンB(1, -1, 1)はどうかな。これ覚えてると思う? これどう、覚えてる? 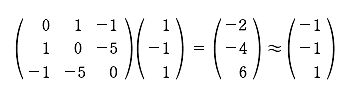 ── 生徒 (-1 , -1 , 1)だから……。 そう、(-1 , -1, 1)だから、パターンB(1, -1, 1)とはちがう物が出てきちゃったね。でも、最後の2つの成分だけに着目してみて。この部分は覚えてるでしょ。これはどういうことかというと、記憶が完璧じゃなかったんだ。何でかというと、パターンBは2回しか教えてないんだな。パターンAは3回やったでしょ。学習の回数が多ければ多いほど、しっかり思い出せるんだね。2回しか覚えてないほうが、混在しているほかの記憶に邪魔されて中途半端にしか思い出せない。なんだか人間にそっくりだ。これがこの脳モデルのひとつ目のポイントね。 でも、もうひとつポイントがあるんだ。それは「推理」という思考過程だ。 たとえば、思い出したいのに情報が完璧じゃないときもあるわけ。後ろ姿だけをみて、その人が誰かを当てるように、一部の情報から全体を推測することって普段の生活でもよくあるよね。 例えばこの脳モデルで、パターンA(1, 1, -1)を思い出したい。でも、(1, 1, ?)、うーん最後の部分は何だっけ、よくわかんないって場合。そういうときには、よくわからない部分を どっちつかずの数字「0」を使うんだ。(1, 1, 0)。そしたらどうなる? 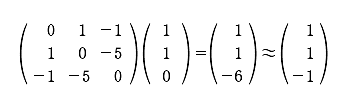 ほら思い出したね。つまり、不完全な情報から全体を補完できるんだ。 こんな単純な、たった3つの神経細胞と、「ヘブの法則」を使っただけで、神経回路は、ちゃんと記憶できるし、思い出せる。勉強不足だと誤って思い出したりもする。さらには推測することさえもできる。行列という数式から、おどろくほどの曖昧性と柔軟性が生まれて、いかにも脳らしいプロセスが現れてくるんだ。「数理ネットワーク」に潜在した可能性を実感できるよね。 もちろん、この脳モデルは単純すぎる。脳の神経は3つだけじゃないし、シナプスもたった6個じゃない。実際にはものすごくいっぱいある。1000億個の神経と1000兆個のシナプスだ。だからまあ、脳がいろいろと複雑な芸当ができても、そりゃ当たり前だとさえ言えるわけだ。 参考事項 現在、この数理モデルを拡張した研究を推進中。成果をまとめて投稿論文を準備しています。 |